Bill Hanawalt

Journal 1

 

The Geometric Building of the Real Number Line

 

A fundamental part of Geometry is the real number line. In this article we are going to go through a step by step building of the real number line. One of the important consequences of being able to use the real number within geometry is the ability to look at geometry analytically (Greenberg 98). This allows us to attach number to distances, for example the length of a segment or the distance between two parallel lines. Another consequence of the reel number line is the ability to talk about geometry algebraically. We can now represent such shapes as circles with an algebraic equation. Now we’ll begin with the building of the real number line.

 

First we are going to build the counting numbers:

 
    1. Using Incidence Axiom I and II we know that a line, we’ll call X, exists. We are also given that two unique points are incident with X, call these two points A0 and A1. As we build points in this sequence they will be built such that AN-1*AN*AN+1.
    2. Given Congruence Axiom I, we know a unique point A2 on X exists, such that A0A1@ A1A2.
    3. Given Congruence Axiom I, A1 a unique point A3 on X, such that A1A2@ A2A3.
    4. Continuing in this pattern, we know a unique point AN exists, such that AN-2AN-1@ AN-1AN. We can continue to do this as N goes to infinity.

      5.  

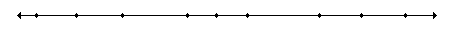      A-N-1 A-N A-N+1 A-1 A0 A1 AN-1 AN AN+1

       

    5. Similarly we can build points, such that A-N-1*A-N *A-N+1, which will represent the negative counting numbers. Given Congruence Axiom I we know that a unique point A-1 exists, such that A-1A0@ A0A1. We can continue to build unique points AN as N goes to negative infinity.
    6. Since we know that AN-2@ AN-1, AN-1@ AN, AN@ AN+1, for all N, by Congruence Axiom II each of these segments are congruent to the others.

Now we can look at each point, labeled AN, as the counting number N.

 

Next we are going to build all the numbers on our number line that can be represented as a fraction. To do this we are going to prove the fact, given two similar triangles (ABC ~ A'B'C'), then the ratio of the length of their corresponding sides are equal (AB/A'B' = BC/B'C' = CA/C'A'). So first lets prove the previous statement about similar triangles. Note that in this section when a segment (AB) is underlined (AB)this corresponds with the numerical length of the segment AB.

 
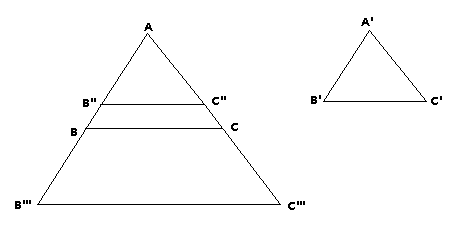
    1. First we are going to build B'' on AB, such that AB''@ A'B' and C'' on AC, such that AC''@ A'C', by Congruence Axiom I.
    2. We know D AB''C''@ D A'B'C', because of SAS:
    1. AB''@ A'B' (step I.).
    2. AC''@ A'C' (step I.).
    3. < A@ < A' (given).
    1. We know < B''@ < B, by congruent parts of congruent triangles, then B''C'' must be parallel to BC, by Theorem 4.1 and alternate interior angles.
    2. Next we build a line M through point A parallel to B''C'', by Theorem 4.1 Corollary II.
    3. Now we extend AB and build point B''', such that B''B'''@ AB.
    4. Now we build a line through B''', called L, parallel to M. We also extend line AC so that it intersects L and call this point C’’’. We know that C''C'''@ AC, because C''D@ B''B''' and because angles are congruent by parallelograms in Euclidean Geometry.
    1. Know by using the Parallel Projective Theorem we know AB''/B''B'''@ AC''/C''C'''. But we also know B''B'''@ AB and C''C'''@ AC, thus AB''/AB@ AC''/AC (Greenberg 170).
    2. Now we start over with our two triangles and repeat steps I through VII, except this time we start by building points C'' on AC, such that AC''@ A'C' and B' on BC, such that BB''@ B'C'.
    3. By repeating those steps we get AC''/AC@ BB''/BC and we already have AB''/AB@ AC''/AC, thus they are all congruent.
    4. The final step is replacing AB'' with A'B', AC'' with A'C', and BB'' with B'C', by congruent parts of congruent triangles and remembering the fact that congruent segments have congruent lengths by theorem 4.3 (Greenberg 123). This gives us AB/A'B'@ BC/B'C'@ CA/C'A'.

 

 

Now that we have proven if we have similar triangles, then the ratio of the length of their coresponding sides are equal, we can build the decimals, which can be represented as fractions on our number line. First we are going to do the specific case of build the fractions a *(1/2), as L ranges from negative to positive infinity (the * represents multiplication).

    1. First we build line Y ^ X at point A0, by Proposition 3.16.
    2. Next we construct point B0 above point A0 on line Y, such that A0B0@ A0A1, by Congruence Axiom I.
    3. Then below point A0 we create point B1, such that A0B1@ A0A1, once again by Congruence Axiom I.
    4. Now we are going to build line Z ^ Y at point B1, by Proposition 3.16.
    5. On Y we are going to build points C1, C2, . . . c¥ to the right of point B1 and points C-1, C-2, . . . C-¥ to the left of point B1, such that Ca -1Ca @ A0A1, by Congruence Axiom I.

      6.  

       

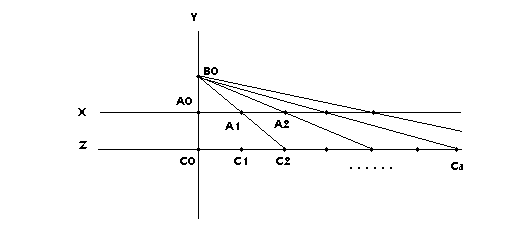
    6. Now construct segments B0C1, B0C2, for all Ca , with each segment B0Ca intersecting X at C'a .
    7. Now consider D B0B1C1 and D B0A0C'1. These triangles are similar, because < B0@ < B0 (same angle), < B1@ < B0 (converse theorem 4.1), and < C1@ < C’1 (converse theorem 4.1). Thus their sides are in ratio to each other. This can be done for every set of triangles, D B0Ca -1Ca and D B0C'a -1C'a .
    8. We also now that each of the smaller triangles side C’a -1C’a are congruent to each other, because each set of similar shares a side with the next to it. We also now that C'a -1 + c'a = 1 and since C'a -1@ C'a , thus C'a must represent the point a /2.

This completes all our points that are multiples of one half. So now we are going to generalize this so we can build all the multiples of 1/x as x goes to infinity.

    1. We add points to Y, below A0, Ba as a goes to x-1 (this x is as in 1/x), such that Ba -1Ba @ A0A1.
    2. Next we build a ^ to Y at Bx-1. Let us call this line Zx-1.
    3. On Zx-1 we build points C-¥ to C¥ , except point C0, which is our Bx-1, such that Ca -1Ca @ A0A1.
    4. Then we build segment B0Ca , for all a , intersecting X at C'a .
    5. Now using our similar triangle technique from the case of x = 2, we are able to see that we have built the points C'a such that it is equal to the value a /x.
    6. Now we can do this for x as it goes to infinity, which gives us all the decimal numbers that can be represented as a fraction.

 

Our final step in completing the real number line is constructing those number, which are not represented by whole numbers or fractions. Examples of these numbers are e, p , and the square root of two. We use the fact that we now continuity holds with in Euclidean Geometry, by Dedekind’s Axiom (Greenberg 98). For example we will construct the square root of five. Let T1 equal the set of x contained in X such that x2 is less then 5 and T2 equal the set of x contained in X such that x2 is greater then 5. Then Deadkind’s Axiom implies that there exists a x0 equal to the square root of 5. You can apply Deadkind’s Axiom in a similar fashion for all real numbers that aren’t represented by whole or fractional numbers.

 

We have now constructed the real number line in Euclidean Geometry. This allows us to use a coordinate system, which intern gives us the ability to look at geometry in a number of new lights, including the use of functions to describe geometric shapes and more broadly to look at Euclidean Geometry numerically.